Interaction of Plasma and E M Waves Easy Language
Abstruse
An electromagnetic (EM) pulse falling on a plasma medium from vacuum can either reflect, get absorbed or propagate inside the plasma depending on whether it is overdense or underdense. In a magnetized plasma, however, there are usually several pass and stop bands for the EM wave depending on the orientation of the magnetic field with respect to the propagation management. The EM wave while propagating in a plasma tin can also excite electrostatic disturbances in the plasma. In this work Particle-In-Cell simulations have been carried out to illustrate the complete transparency of the EM moving ridge propagation inside a strongly magnetized plasma. The external magnetic field is chosen to be perpendicular to both the moving ridge propagation management and the electric field of the EM wave, which is the X mode configuration. Despite the presence of charged electron and ion species the plasma medium behaves like a vacuum. The ascertainment is understood with the help of particle drifts. Information technology is shown that though the two particle species move under the influence of EM fields their move does non lead to any charge or current source to change the dispersion relation of the EM moving ridge propagating in the medium. Furthermore, it is also shown that the cease band for EM wave in this regime shrinks to a zero width as both the resonance and cutting-off points approach each other. Thus, transparency to the EM radiation in such a strongly magnetized case appears to exist a norm.
Introduction
A wide range of intense magnetic fields be in astrophysical (e.g. in galaxy clusters, shock formation in gamma ray bursts, magnetosphere of neutron starsiii,four,5,6) as well as in the laboratory plasmas7. On one paw there has been several ongoing enquiry to generate intense magnetic fields in the laboratory, while on the other, several instabilities lead to the generation of intense magnetic field in cosmological infinite (due east.g. magnetic field generation via Kelvin-Helmholtz instability, counter-streaming electron flows etceight,9,10). These magnetic fields can be very potent, for instance, virtually pulsars and magnetars they could exist of the lodge of Giga Teslas11,12,thirteen and a record magnetic field of 1.2 KT has been accomplished in the laboratoryvii. It is thus important to study interaction of an electromagnetic wave with a strongly magnetized plasma for both laboratory as well as astrophysical contextone,2 xiv,15,16. The principle mechanisms in plasmas depend on EM wave frequency and plasma permittivity. Plasma permittivity can be altered by suitably choosing the plasma density and applied magnetic field. The costless charges and their associated currents in the plasma medium human activity equally sources and influence the plasma dielectric constant. Propagation of EM wave through strongly magnetized plasma sources, therefore, needs to be understood.
The upshot of EM moving ridge achieving complete transparency is important and has been considered earlier in many contexts. An attempt to reach transparency using strong fields generated by intense femto-second (fs) laser pulse has been studied past17,18,nineteen,20,21. Total transmission was observed when 30 fs light amplification by stimulated emission of radiation pulse of intensity \(iii\times x^{18}\) Due west \(\text{cm}^{-2}\) passes through \(0.1 \; \upmu\)m plastic foil targetsxviii. This mechanism is operative when the target width is much smaller than the light amplification by stimulated emission of radiation wavelength17. Still, for thick targets, relativistic laser would lead to excitation of coherent structures and/or instabilities leading to turbulence in the system22,23.
External magnetic fields have been applied in several contexts to achieve transparency. The dressing of resonance states for RHCP (Right Manus Circularly Polarized) waves with the combination of axial and wiggler magnetic field is attempted to larn a window of transparency in the opaque magnetized plasma for the EM moving ridge24. Another technique to seek transparency is by employing pump electromagnetic wave to transmit the probe wave25,26,27,28. This method is coordinating to a quantum mechanical phenomena known equally EIT (Electromagnetically Induced Transparency). In this phenomena, an electromagnetic wave is fabricated to propagate in ordinarily opaque medium in presence of powerful secondary EM waves. This is possible due to the destructive interference betwixt several energy levels connecting the ground and excited states of the atom. This method is heavily used in not-linear optics to dispense the energy levels of diminutive states or slow down the waves29,30,31. In plasma, the use of pump and probe EM moving ridge is used to make plasma transparent to RHCP moving ridge. Simply this report is express to propagation of RHCP waves along the magnetic field lines and generating an additional wiggler magnetic field is a complexity from application viewpoint. More than chiefly these methods focus on R-wave mode where propagation is along the magnetic field, while L-moving ridge and X-mode propagation geometries are yet to be explored.
We take carried out Particle-In-Cell simulations to study the propagation of EM wave in a strongly magnetized plasma for which both the electron and ion species are strongly magnetized. An interesting observation of complete transparency of the plasma medium is observed for the propagation of EM wave in the X mode configuration. The width of the stop band of the X mode reduces to zero and a completely transparent propagation of EM wave is observed. For X-fashion, dispersion bend is given in Fig. i, there are two cease bands (\(\omega _{LH}-\omega _{L}\) and \(\omega _{UH}-\omega _{R}\), where LH,UH,50,R stands for Lower Hybrid, Upper Hybrid, Left Manus Cutoff, Correct Hand Cutoff respectively). Whenever laser/EM moving ridge frequency lying on these bands is incident on plasma, information technology generates a shielding electric field in response to avert penetration of EM wave inside it. The propagation of EM wave in plasma thus depends on the intensity and/or frequency of the incident EM moving ridge. We show that when the stiff external magnetic field dominates the motion of both charged species, i.e. \(\omega _{ce}> \omega _{ci} > \omega _{fifty}\), or it strongly magnetizes electrons but the perturbations are at faster time scales than that of ions \(\omega _{ce}> \omega _{l} > \omega _{L}\), the electromagnetic moving ridge propagates undisturbed inside plasma. The inequalities gives an insight to plasma in terms of anisotropy and modification in its collective behaviour that gets affected by introduction of magnetic field. Such caveats are vital for absorption phenomena too.

Dispersion of X-way when \({\vec {thou}} \perp {\vec{B_0}}\), classified into three regions. The numbers on the right manus side represent to resonance and cutoff frequencies for \(m_i=100m_e\) in normalized units.
A stiff magnetic field in which the two charged species remain closely tied to the magnetic field at the EM wave frequency, ensures that they do not provide the plasma a chance to answer to the incoming laser/EM wave. Nosotros show that equally the strength of magnetic field increases, the magnitude of self generated fields in bulk plasma due to interaction of laser with plasma decreases and the EM wave propagation speed inside the plasma approaches the speed of calorie-free c. The plasma medium thus acts transparent to the incoming EM moving ridge. These observations would have of import implications in astrophysics. For instance, the forcefulness of magnetic field in neutron stars and magnetars are very loftier of the order of Giga-Tesla. Plasma medium near these astrophysical objects would hands be in strongly magnetized authorities for our results to be applicative for visible and even college frequency radiations.
Simulation details
We accept carried out series of one dimensional (forth \(\hat{10}\)) Particle In Prison cell(Pic) simulations in X-mode configurations using OSIRIS-four.032,33,34. For X-mode configuration, compatible external magnetic field (\(B_0(m_e\omega _{pe}c/e)\)) has been applied in \(\chapeau{z}\) direction. A uniform plasma density comprising of electrons and ions has been considered. Ion mass is taken to be 100 times mass of electrons (\(m_i=100m_e\)) for faster computation. Plasma boundary extends from \(x=850 c/\omega _{pe}\) to \(x=2000c/\omega _{pe}\) whereas total length of simulation box is \(3000 c/\omega _{pe}\). Boundary condition for particles as well as fields are absorbing, with spatial and temporal grid taken to be 0.05 and 0.02 respectively. A p-polarized, plane laser pulse is incident normally at plasma (\(n=3.14 \times 10^{20}\) c.c) from the left boundary. These values of plasma density volition differ with EM moving ridge frequency for dissimilar region of 10-mode according to ratio given in Table 1. Laser is propagating along \(\lid{x}\) with its spatial profile centered at \(x= 450 c/\omega _{pe}\) and ranging from \(x= 0\) to \(800 c/\omega _{pe}\). We also want to analyze that this work focuses on proof of concept so the mechanism presented in this paper depends on the magnetization of the accuse species with respect to the incoming EM pulse frequency. We take carried out a parametric study on magnetic fields such that broadly they follow either criteria I (\(\omega _{ce}> \omega _{50} > \omega _{ci}\)) or criteria II (\(\omega _{ce}> \omega _{ci} > \omega _{50}\)). This parametric study has been done with laser pulse of intensity lying in non-relativistic regime such that amplitude of laser electric field (\(E_0=0.03(m_e \omega _{pe}c/e)\)) is constant for all runs. This has been washed to avert other relativistic machinery to play a role. A schematic of simulation geometry has been shown in Fig. 2. Dissimilar laser frequency maintaining criteria I and criteria Ii has also been chosen co-ordinate to frequency which is explained more than elaborately in side by side section. A tabular form of simulation parameters is given in Tabular array 1.
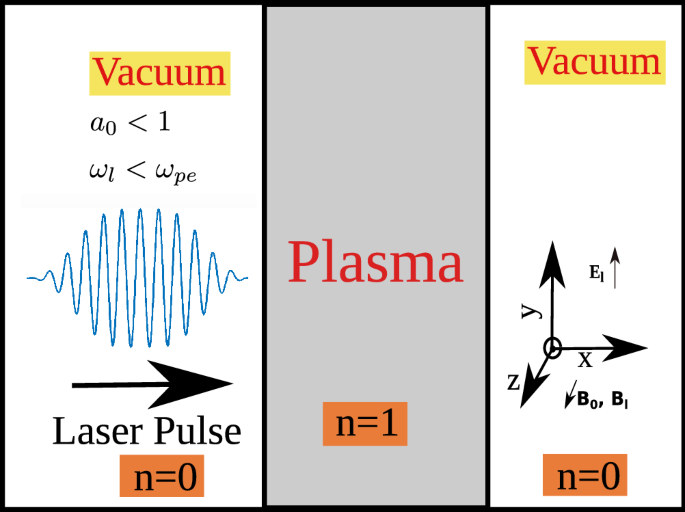
Schematic of simulation geometry [not to scale]. Plasma slab is placed in vacuum, management of external Magnetic field (\(B_0\)) is forth the aforementioned management equally that of the magnetic field of laser (\(B_l\)) i.e. \(\hat{z}\). Electric field of laser is forth \(\hat{y}\) direction. \(a_0\) is normalized vector potential i.eastward. (\(eE_0/one thousand\omega c\)). This parameter decides the regime of plasma dynamics, in this work we have taken \(a_0<1\) i.e. non-relativistic authorities. In this schematic, 'n' denotes plasma density.
Results
Theory and analytical cess
It is well known that when EM moving ridge is propagating perpendicular to external magnetic field, plasma supports ii kinds of waves, O-way (ordinary wave) and boggling mode (Ten-mode). O-mode is contained of applied magnetic field (ordinary moving ridge). The full general dispersion relation for perpendicular propagation in common cold plasma (\(\mathbf {k}\perp \mathbf {B}\)) is given by the matrix35,
$$\begin{aligned} \begin{bmatrix} Southward &{} -iD &{} 0\\ iD &{} South-due north^2 &{} 0\\ 0 &{}0 &{} P-northward^ii \end{bmatrix} \begin{bmatrix} E_x\\ E_y\\ E_z \end{bmatrix}=0 \end{aligned}$$
(1)
where, \(Due south=\frac{ane}{two}\left( R+L\right)\), \(D=\frac{1}{2}\left( R-L\right)\), \(P=1-\frac{\omega ^2_{p}}{\omega ^ii}\)
$$\begin{aligned}&R=1- \frac{\omega _{pe}^2 + \omega _{pi}^2}{(\omega + \omega _{ci})(\omega - \omega _{ce})} \end{aligned}$$
(2)
$$\brainstorm{aligned}&Fifty=1- \frac{\omega _{pe}^2 + \omega _{pi}^2}{(\omega - \omega _{ci})(\omega + \omega _{ce})} \end{aligned}$$
(3)
The X-mode has cut-offs at \(\omega _R\) and \(\omega _L\) respectively. \(\omega _R\) and \(\omega _L\) are given as follows:
$$\begin{aligned} \omega _{R,L}= [\omega _{pe}^2+\omega _{pi}^2+(\omega _{ci}+\omega _{ce})^2/4]^{ane/2} \mp (\omega _{ci}-\omega _{ce})/two \end{aligned}$$
(four)
Dispersion curve of 10-mode is shown in Fig. 1. We accept labelled dispersion curve into three regions depending on the dominant function played past the species. Region I is dominated past dynamics of ions and Region 3 by electrons. Region II is stop ring every bit it lies betwixt \(\omega _{LH}\) (resonance point) and \(\omega _{L}\) (cut-off point).
Dispersion relation for X-mode is obtained,
$$\begin{aligned} n^ii= \frac{RL}{Due south} \end{aligned}$$
(five)
where, n is refractive alphabetize. Resonance occur when \(S \rightarrow 0\)
$$\brainstorm{aligned} \omega ^iv-\left( \omega _{pe}^2+\omega _{pi}^2+\omega _{ce}^2+\omega _{ci}^ii\correct) \omega ^2+\omega _{ci}^two\omega _{ce}^ii+\omega _{pe}^ii\omega _{ci}^2+\omega _{pi}^2\omega _{ce}^2=0 \end{aligned}$$
(six)
This is a bi-quadratic equation, it's lower end solution is plotted as function of applied magnetic field in Fig. 4. As can exist seen from the figure, when \(B_0<10\) (at \(B_0=10, \omega _{ci}=\omega _{pi}\)) it falls in criteria I and solution of Eq. (6) matches perfectly with reduced expression of \(\omega _{LH}\). At higher magnetic fields, \(\omega _{LH}\) saturates at \(\omega _{pi}\) while solution of Eq. (6) approaches left manus cut off (\(\omega _{L}\)) asymptotically which concludes that at this college magnetic field the resonance bespeak and cut off approach each other thus effectively reduce the width of the stop band. This was checked by simulation as well for frequency parameter lying in region Two (i.e. stop ring). Under criteria I, laser reflected dorsum. On the other hand, under criteria II laser pulse was able to propagate through the plasma. This was possible due to effective reduction of stop ring and resonance indicate lying well above EM frequency. And so, effectively this case does non lie in region Two simply in region I.
In Fig. 3, we have plotted the dispersion curve for X-mode in ii criteria. As 1 can observe from the left subplot that in criteria I, all the regions are well separated while in the criteria Two stop band has shrunk. Moreover, the dispersion follows \(\omega =g\) (as \(c=one\)). Therefore, it rules out whatsoever other mode excitation when \(\omega _{ce}> \omega _{ci} > \omega _{l}\).

Dispersion curve for ii criteria [criteria I \((\omega _{ce}>\omega _l>\omega _{ci})\) and criteria Ii (\(\omega _{ce}>\omega _{ci}>\omega _{l}\)) are shown in subplot (a) and (c) respectively]. In subplot (b) and (d), we expand the dispersion curves shown in (a) and (c) respectively. From these curves, we tin can detect that while criteria I has two finish bands and iii pass bands, criteria II dispersion has \(\omega =ck\) all forth.
To summarize our propagation characteristics according to their region of dispersion curve in Fig. 1 is given in Table 2.
Detail quantitative assay to summate assimilation (A), reflection (R), transmission (T) coefficients has too been done which is presented hither in tabulated course (Table 3).
Ane comment should be fabricated hither about another solution in the upper finish of frequency scale, it was found that at high magnetic field region \(\omega _{ce}\) dominates all modes and cut off points and hence they merge very well. Plot of verbal solution of Eq. (6) equally function of \(B_0\) practical is given in Fig. 4. As one can observe here gap betwixt \(\omega _R\) and \(\omega _{UH}\) is very thin and at loftier magnetic fields they also merge indicating that stop band at upper frequency also vanishes with application of potent magnetic field.

(A) Comparing of lower exact solution for \(\omega\) (Eq. 6) with cut off frequency and belittling expression of LH as part of \(B_0\). Every bit one can observe that at lower magnetic field value, in that location'southward gap between values of \(\omega _{L}\) and \(\omega _{LH}\) but at high value of magnetic field where exact solution of \(\omega\) volition play a role, it matches with \(\omega _{50}\); signifying the shrink of cease band. Light-green dash-line indicates the \(\omega _{pi}\) position in the plot. (B) Comparison of upper exact solution for \(\omega\) with cut off frequency and analytical expression of UH as role of \(B_0\). Every bit one tin can observe that at lower magnetic field value there's gap between values of \(\omega _{R}\) and \(\omega _{UH}\) but at high value of magnetic field where verbal solution of \(\omega\) volition play a function it matches with \(\omega _{R}\) indicative to the vanishing of terminate band.
\(\omega\) and \({thou}\) analysis
In whatsoever dispersive medium, as the refractive alphabetize of media modify spatially, the frequency of the EM moving ridge remains same while its wavelength suffers a change. In this section we calculate the modified k and the phase velocity of incident laser pulse. We observe that by varying ambient magnetic field, phase velocity of laser pulse also changes (approaches velocity of light in vacuum, c) while decreasing the perturbations in the plasma.
Figure 5 shows a comparing of all 3 cases lying in Region I. Initially (at t = 0), electric field due to laser is present in the system. In case (A) (\(B_0=0\)), the light amplification by stimulated emission of radiation interacts with plasma and gets reflected dorsum from the plasma surface. However, for case (B) (\(B_0 = 3\), satisfying the condition \(\omega _{ce}> \omega _{l} > \omega _{ci}\)), there are certain modes generated in plasma and as a result we observe a finite magnitude of \(E_x\) in the organisation i,2. \(E_x\) that become generated in plasma take higher magnitude than \(E_y\). On the other hand, in instance (C) (\(B_0=20\), satisfying the status \(\omega _{ce}> \omega _{ci} > \omega _{l}\)), the plasma seems to be completely undisturbed by the laser as pulse freely propagates inside it without creating whatever perturbations in the medium and goes into vacuum space in the right side. The transparency induced in plasma on applying external magnetic field is the key observation of this work. Plasma density plots evidence that in case (A), plasma density at the interface is modified, on the contrary, for case (B), density perturbations are present in the bulk plasma likewise. Ion density fluctuates more than electrons which propagates in longitudinal direction as can exist seen at later times in Fig. 6. For case (C), there being density perturbations that can be seen at \(t =500\) is due to laser field i.eastward. electrons and ions fluctuates with same aamplitude, justifying our observation that laser remains undisturbed via interaction with plasma in this case (Fig. vi).

Spatial variation of \(E_x\) and \(E_y\) for the three cases at different times. Initially, only \(E_y\) (due to light amplification by stimulated emission of radiation field) is present in the system. In case (A), laser gets reflected from the plasma purlieus without being able to interact with it. On the other hand, laser is able to interact with plasma in instance (B) and we discover generation of \(E_x\) in the system. In example (C), medium becomes transparent to laser and light amplification by stimulated emission of radiation just passes through the plasma medium unhindered.
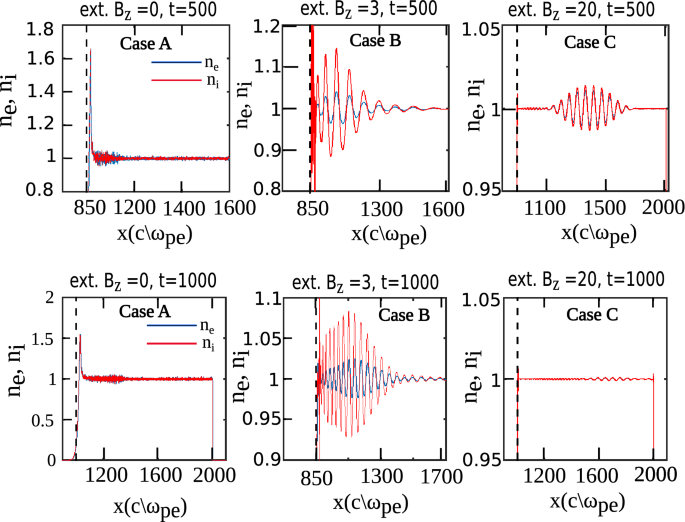
Spatial variation of number density of electrons and ions for the iii cases at different times showing that plasma density gets perturbed at the interface for example (A) whereas for case (B), nosotros observe density fluctuations in the majority plasma likewise which retain themselves fifty-fifty after laser has moved out of the simulation box (\(t=g\)). For case (C), on the other hand, we observe some density perturbations in the majority plasma at the fourth dimension of interaction with laser (\(t=500\)) but these fluctuations are not retained by plasma after the interaction with light amplification by stimulated emission of radiation is over.
Figure vii shows the Fast Fourier Transform (FFT) of \(B_z\) of light amplification by stimulated emission of radiation with respect to time for four dissimilar value of magnetic field, where transparency has been induced. It can be seen that the frequency of laser (\(\omega _l=0.2\)) does not change while propagating inside plasma (we show FFT of \(B_z\) with fourth dimension at ii different values of x in the majority plasma and obtain the same peak). However, \(k_x\) of EM wave gets modified on propagation inside plasma (Fig. 8). The shift from the initial value of \(k_x\) decreases on increasing practical magnetic field. We calculate the modified velocity of EM wave in plasma by peak frequency of the wave from the FFT and modified \(k_x\) value (method II in Table four) and found that velocity of the moving ridge inside plasma approaches to c on increasing applied magnetic field (Table four). In Tabular array 4, we calculate velocity by two methods. In method I, we choose a point on the waveform and summate the fourth dimension taken past that indicate to embrace a detail distance and method II includes calculation of velocity by modification in \(k_x\). Then nosotros conclude that stiff magnetization can end pulse modification while pulse waveform is propagating through plasma media.

Fast Fourier Transform (FFT) of \(B_{z}\) with time at ii different locations in majority plasma, showing that the peak frequency of electromagnetic wave does not change and it propagates unhindered in the plasma medium for dissimilar magnetic fields (\(B_0=viii, 15, twenty, forty\)).

FFT of \(B_{z}\) with x at different times showing that as laser interacts with plasma, \(k_x\) shifts to a larger value than the initial \(k_x\). This shift reduces as we increase the magnitude of applied magnetic field (shown in different subplots). This shift in \(k_x\) is also reflected in velocity of EM wave approaching c in the medium (Table 4) and the transmission coefficient approaching unity (Table 3).
Reversible and irreversible exchange of free energy
In this study, nosotros observed that depending on region and criteria, the laser energy substitution is either reversible or irreversible. As one can detect from Table 3, in region I criteria I at that place is pregnant absorption and this region is well explored in ref1. From these studies we know that in region I criteria I free energy is dominantly coupled to ions and this coupling process is irreversible. While in region I criteria II, due to transparency, energy transfer is observe to be reversible. As when laser is nowadays in the plasma, electrons and ions oscillate due to oscillating electric field and when the field passes through, they come to rest. In region II criteria I, laser reflects dorsum due to germination of shielding fields so in that location'due south no exchange of energy altogether. On the other hand region II criteria II is finer Region I criteria 2 so in that location's similar substitution of energy which is reversible.
In region Three criteria I, nosotros discover \(97 \%\) transparency and reversible exchange of free energy. This is quite dissimilar from other two regions, the reason behind this is uncomplicated. As the fourth dimension scales of region III are same as electrons, with \(B_0=3\) electrons are strongly magnetized. And then that's why laser is non able to couple its energy into electron effectively. To couple laser energy into electron irreversibly ane has to weakly magnetize the electron and that tin can be accomplished by ensuring another inequality i.eastward. \(\omega _{ce}<\omega _{fifty}<\omega _{Fifty}\). When we simulated with this status past taking \(B_0=0.25\), nosotros observe \(10.two\%\) absorption into electrons and about \(2.2\%\) energy to ions irreversibly while \(88 \%\) of light amplification by stimulated emission of radiation pulse was reflected back.
Therefore, when the species are tightly bound to external magnetic field, they are not able to take free energy from EM pulse irreversibly. That's why in region I and criteria Two when both the species were tightly magnetized to external magnetic field they were unable to couple their motility to laser pulse and that's how pulse was transparent in this medium. In region Three where it is in propagating region when electrons were tightly bounded we observe transparency for similar reason. One can contend that ions are not magnetized in this status but this region'south time scales are fast then only electron motion is important here.
Now we move on to demonstrate the effect of charge separation on irreversible energy coupling. Nether the effect of oscillating electric field and external magnetic field, the longitudinal drift tin can exist written by Eq. (vii)
$$\begin{aligned} {\vec{V}}_{\vec {E} \times {\vec{B}}}(t) = \frac{ \omega _{cs}^2}{ \omega _{cs}^2 - \omega _{l}^2} \frac{ {\vec {E}}(t) \times {\vec{B}}}{B^ii} \end{aligned}$$
(vii)
Here, the suffix \(south = e, i\) represents the electron and ion species respectively. In Criteria II, both ions and electrons are strongly magnetized and the dynamics are governed by the Lorentz force i.e. Eq. (vii). Every bit longitudinal velocity is independent of mass of the species for this criteria, in that location's no possibility of charge separation such that there are no shielding fields to restrict the EM pulse propagation. A comparative assay has been done between analytical migrate given in Eq. (7) and numerical longitudinal drift experienced past both ion and electron in subplot (B) of Fig. 9 and it can be observed that in that location'southward no velocity divergence between species which results in no net charge density separation and hence EM wave is able to propagate unhindered. In Criteria I, electrons follow Eq. (seven) while ion motion is governed by electric fields as they are unmagnetized. This is shown in subplot (A) and (C) of Fig. 9. We observe that they lucifer well. When \(\omega _{ce}<\omega _{l}\) (named as Criteria 0), both species are unmagnetized and they follow the longitudinal electric field (run into subplot (D) of Fig. 9).

Comparison of electron and ion drift theoretically (Eq. seven) and simulation results. In criteria Two both species are magnetized and their drift velocity in longitudinal management is also same such that in that location'southward no charge separation which can inhibit the propagation of EM wave (B). In the case when \(\omega _l>\omega _{ce}\), in that location's generation of electrostatic perturbation which helps in coupling laser free energy into plasma irreversibly shown in subplot (D). For criteria I in region I and Iii, ions are un-magnetized while electrons are tightly jump to magnetic field [in subplot (A) and (C)].
For a finite electromagnetic pulse the plasma species (electron and ions) too experience the ponderomotive pressure. The difference between the ponderomotive force experienced by electron and ions can lead to electrostatic excitations. However, information technology has been shown in ref.36 that in the X-mode configuration the ponderomotive pressure is same for ions and electrons at very stiff magnetic fields. Thus, a finite EM pulse can too propagate undisturbed.
Decision
A particular PIC simulation has been carried out by usa to show consummate transparency of EM moving ridge radiation through a plasma in the presence of strong ambient field. The strength of the magnetic field has to exist strong plenty to arm-twist magnetized response from both electron and ion species at the EM moving ridge frequency. The effect does non crave relativistic intensity of the EM moving ridge. This report finds information technology's relevance in many fields of awarding where deposition and transfer of EM free energy is required. This is achieved by appropriately tailoring the magnetic field arrangements to ane's desirability. Such special configured magnetic fields are useful in field of optics where pulse modulation is undesirable. This written report can be of relevance in the plasma stealth technology. More rigorous studies are required in this regard to comment any further. Nosotros feel that these observations will take important significance in the context of astrophysical plasma almost pulsar and magnetars where the magnetic field is quite strong and would elicit magnetized plasma response for typical EM frequencies of interest. In determination, our study proves that, under external magnetic effects, plasma can lose its collective behaviour.
References
-
Vashistha, A., Mandal, D., Kumar, A., Shukla, C. & Das, A. A new mechanism of direct coupling of laser energy to ions. New J. Phys. 22, 063023. https://doi.org/10.1088/1367-2630/ab8cad (2020).
-
Vashistha, A., Mandal, D. & Das, A. Excitation of lower hybrid and magneto-sonic perturbations in laser plasma interaction. Nucl. Fusion 61, 026016. https://doi.org/10.1088/1741-4326/abcc1a (2021).
-
Medvedev, Thou. V. Electron acceleration in relativistic gamma-ray burst shocks. Astrophys. J. 651, L9–L11. https://doi.org/10.1086/509075 (2006).
-
Vikhlinin, A., Markevitch, M. & Murray, Due south. S. [ITAL]chandra[/ITAL] gauge of the magnetic field strength virtually the cold front end in a3667. Astrophys. J. 549, L47–L50. https://doi.org/10.1086/319126 (2001).
-
Vogt, C. & Enßlin, T. . A. . Measuring the cluster magnetic field power spectra from Faraday rotation maps of Abell 400, Abell 2634 and Hydra A. A&A 412, 373–385. https://doi.org/10.1051/0004-6361:20031434 (2003).
-
Taylor, Yard. B., Fabian, A. C. & Allen, S. Westward. Magnetic fields in the Centaurus cluster. Mon. Notices R. Astron. Soc. 334, 769–776. https://doi.org/10.1046/j.1365-8711.2002.05555.10 (2002).
-
Nakamura, D., Ikeda, A., Sawabe, H., Matsuda, Y. H. & Takeyama, S. Record indoor magnetic field of 1200 t generated by electromagnetic flux-compression. Rev. Sci. Instrum. 89, 095106. https://doi.org/10.1063/1.5044557 (2018).
-
Medvedev, Thou. V., Silva, L. O. & Kamionkowski, One thousand. Cluster magnetic fields from large-scale construction and milky way cluster shocks. Astrophys. J. 642, L1–L4. https://doi.org/ten.1086/504470 (2006).
-
Alves, E. P. et al. Large-scale magnetic field generation via the kinetic Kelvin-Helmholtz instability in unmagnetized scenarios. Astrophys. J. 746, L14. https://doi.org/10.1088/2041-8205/746/2/l14 (2012).
-
Alves, E. P., Grismayer, T., Fonseca, R. A. & Silva, L. O. Electron-scale shear instabilities: Magnetic field generation and particle acceleration in astrophysical jets. New J. Phys. sixteen, 035007. https://doi.org/10.1088/1367-2630/16/3/035007 (2014).
-
Mazur, D. & Heyl, J. S. Non-linear electromagnetic waves in magnetosphere of a magnetar. Mon. Notices R. Astron. Soc. 412, 1381–1388. https://doi.org/10.1111/j.1365-2966.2010.17995.x (2011).
-
Parent, D. et al. Observations of energetic high magnetic field pulsars with the fermi large area telescope. Astrophys. J. 743, 170. https://doi.org/ten.1088/0004-637x/743/2/170 (2011).
-
Camilo, F. et al. Discovery of two loftier magnetic field radio pulsars. Astrophys. J. 541, 367–373. https://doi.org/10.1086/309435 (2000).
-
Kaw, P. K. & Dawson, J. M. Laser-induced anomalous heating of a plasma. Phys. Fluids 12, 2586–2591. https://doi.org/10.1063/1.1692400 (1969).
-
Dawson, J. & Oberman, C. Effect of ion correlations on high-frequency plasma conductivity. Phys. Fluids vi, 394–397. https://doi.org/10.1063/1.1706745 (1963).
-
Kaw, P. K. Nonlinear laser-plasma interactions. Rev. Mod. Plasma Phys. 1, 15970. https://doi.org/x.1007/s41614-017-0005-2 (2017).
-
Teychenné, D., Giulietti, A., Giulietti, D. & Gizzi, 50. A. Magnetically induced optical transparency of overdense plasmas due to ultrafast ionization. Phys. Rev. East 58, R1245–R1247. https://doi.org/10.1103/PhysRevE.58.R1245 (1998).
-
Giulietti, D. et al. Observation of solid-density laminar plasma transparency to intense xxx femtosecond light amplification by stimulated emission of radiation pulses. Phys. Rev. Lett. 79, 3194–3197. https://doi.org/10.1103/PhysRevLett.79.3194 (1997).
-
Siminos, East., Grech, M., Skupin, Due south., Schlegel, T. & Tikhonchuk, V. T. Effect of electron heating on cocky-induced transparency in relativistic-intensity laser-plasma interactions. Phys. Rev. Due east 86, 056404. https://doi.org/10.1103/PhysRevE.86.056404 (2012).
-
Kulagin, Five. V., Cherepenin, V. A., Hur, Yard. S. & Suk, H. Flying mirror model for interaction of a super-intense light amplification by stimulated emission of radiation pulse with a thin plasma layer: Transparency and shaping of linearly polarized laser pulses. Phys. Plasmas 14, 113102. https://doi.org/x.1063/1.2799169 (2007).
-
Palaniyappan, Southward. et al. Dynamics of relativistic transparency and optical shuttering in expanding overdense plasmas. Nat. Phys. 8, 763–769 (2012).
-
Mandal, D., Vashistha, A. & Das, A. Spontaneous formation of coherent structures by an intense laser pulse interacting with overdense plasma. J. Plasma Phys. 86, 905860606. https://doi.org/10.1017/S0022377820001361 (2020).
-
Chatterjee, Thou. et al. Magnetic turbulence in a table-top laser-plasma relevant to astrophysical scenarios. Nat. Commun. 8, 15970 (2017).
-
Gad, R., Leopold, J. K., Fisher, A., Fredkin, D. R. & Ron, A. Observation of magnetically induced transparency in a classical magnetized plasma. Phys. Rev. Lett. 108, 155003. https://doi.org/10.1103/PhysRevLett.108.155003 (2012).
-
Kawamori, Eastward., Syugu, W.-J., Hsieh, T.-Y., Song, S.-X. & Cheng, C. Z. Experimental identification of electromagnetically induced transparency in magnetized plasma. Phys. Rev. Lett. 108, 075003. https://doi.org/x.1103/PhysRevLett.108.075003 (2012).
-
Shvets, Grand. & Wurtele, J. S. Transparency of magnetized plasma at the cyclotron frequency. Phys. Rev. Lett. 89, 115003. https://doi.org/10.1103/PhysRevLett.89.115003 (2002).
-
Shvets, 1000., Tushentsov, M., Tokman, Grand. D. & Kryachko, A. Propagation of electromagnetic waves in the plasma near electron cyclotron resonance: Undulator-induced transparency. Phys. Plasmas 12, 056701. https://doi.org/10.1063/one.1865053 (2005).
-
Hur, One thousand. Southward., Wurtele, J. S. & Shvets, G. Simulation of electromagnetically and magnetically induced transparency in a magnetized plasma. Phys. Plasmas 10, 3004–3011. https://doi.org/10.1063/ane.1580816 (2003).
-
Boller, K.-J., Imamoğlu, A. & Harris, S. Eastward. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 66, 2593–2596. https://doi.org/10.1103/PhysRevLett.66.2593 (1991).
-
Fleischhauer, M., Yelin, S. & Lukin, 1000. How to trap photons? Storing unmarried-photon quantum states in collective atomic excitations. Opt. Commun. 179, 395–410. https://doi.org/10.1016/S0030-4018(99)00679-three (2000).
-
Harris, S. Due east. Electromagnetically induced transparency with matched pulses. Phys. Rev. Lett. 70, 552–555. https://doi.org/ten.1103/PhysRevLett.70.552 (1993).
-
Hemker, R. Grand. Particle-In-Jail cell Modeling of Plasma-Based Accelerators in Two and Three Dimensions. (Thesis, University of California, 2000). arxiv:1503.00276.
-
Fonseca, R. A. et al. OSIRIS: A Three-Dimensional, Fully Relativistic Particle in Cell Code for Modeling Plasma Based Accelerators 342–351 (Springer, 2002).
-
Fonseca, R. A. et al. One-to-i direct modeling of experiments and astrophysical scenarios: Pushing the envelope on kinetic plasma simulations. Plasma Phys. Control. Fusion l, 124034 (2008).
-
Boyd, T., Boyd, T. & Sanderson, J. The Physics of Plasmas (Cambridge University Press, 2003).
-
Goswami, Fifty. P., Maity, Due south., Mandal, D., Vashistha, A. & Das, A. Ponderomotive strength driven mechanism for electrostatic wave excitation and free energy absorption of electromagnetic waves in overdense magnetized plasma. arXiv preprint arXiv:2104.09320 (2021).
Acknowledgements
The authors would like to acknowledge the OSIRIS Consortium, consisting of UCLA ans IST(Lisbon, Portugal) for providing access to the OSIRIS4.0 framework which is the work supported by NSF ACI-1339893. AD would similar to admit her J. C. Bose fellowship grant JCB/2017/000055 and the CRG/2018/000624 grant of DST for the work. The simulations for the work described in this paper were performed on UDAY and ANTYA, IPR Linux clusters. D.M would like to acknowledge Laxman Prasad Goswami for discussions on ponderomotive drift effects in plasma.
Author information
Authors and Affiliations
Contributions
D.M. and A.D. planned the research; D.M., A.5., and A.D. wrote the manuscript; D.M. and A.V. analyzed the results; D.M., A.Five. and A.D. interpreted the results; A.D. supervised the inquiry.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional data
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open up Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits utilize, sharing, adaptation, distribution and reproduction in any medium or format, as long equally you requite advisable credit to the original author(southward) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party textile in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is non included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted employ, y'all will demand to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/past/4.0/.
Reprints and Permissions
Nigh this article
Cite this commodity
Mandal, D., Vashistha, A. & Das, A. Electromagnetic moving ridge transparency of 10 mode in strongly magnetized plasma. Sci Rep xi, 14885 (2021). https://doi.org/x.1038/s41598-021-94029-three
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/ten.1038/s41598-021-94029-iii
Farther reading
Comments
By submitting a comment you concord to bide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag information technology equally inappropriate.
Source: https://www.nature.com/articles/s41598-021-94029-3
0 Response to "Interaction of Plasma and E M Waves Easy Language"
Post a Comment